lunes, 24 de mayo de 2010
RECONOCER Y DETERMINAR LAS RAZONES TRIGONOMETRICAS EN FAMILIAS DE TRIANGULOS-RECTANGULOS SEMEJANTES (marzo)

Razones trigonométricas
El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo , correspondiente al vértice A, situado en el centro de la circunferencia.
El seno (abreviado como sen, o sin por llamarse "sinus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa,:
sen a = CB//AB = a/c
El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,:
cos a = AC//AB = b/c
La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,:
tan a = CB//AC = a/b
APLICAR EL TEOREMA DE PITAGORAS EN LA RESOLUCION DE PROBLEMAS (marzo)
El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual, a la suma de los cuadrados de las longitudes de los dos catetos (los dos lados menores del triángulo rectángulo: los que conforman el ángulo recto). Si un triángulo rectángulo tiene catetos de longitudes y , y la medida de la hipotenusa es , se establece que:
c2 = a2 + b2
Demostración
Sea el triángulo rectángulo de catetos a y b e hipotenusa c. Se trata de demostrar que el área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y lado b. Es decir:
a2 + b2 = c2
Si añadimos tres triángulos iguales al original dentro del cuadrado de lado c formando la figura mostrada en la imagen, obtenemos un cuadrado de menor tamaño. Se puede observar que el cuadrado resultante tiene efectivamente un lado de b - a. Luego, el área de este cuadrado menor puede expresarse de la siguiente manera:
(a - b)2 = a2 - 2ab + b2
Ya que .
(b - a)2 = (a - b)2
Es evidente que el área del cuadrado de lado c es la suma del área de los cuatro triángulos de altura a y base b que están dentro de él más el área del cuadrado menor:
c2 = 4. (a . b / 2) + a2 - 2ab + b2 = a2 + b2
GRAFICAS DE RELACIONES FUNCIONALES NO LINEALES! (febrero)

Función lineal
Una aplicación lineal (también llamada función lineal, transformación lineal u operador lineal) es una aplicación entre dos espacios vectoriales, que preserva las operaciones de suma de vectores y producto por un escalar. El término función lineal se usa incorrectamente en análisis matemático y en geometría para designar una recta, un plano, o en general una variedad lineal.
Codominio.Son aplicaciones lineales los operadores usados en la formulación matemática de la mecánica cuántica
Sistemas de ecuaciones lineales
Los sistemas de ecuaciones lineales expresan varias ecuaciones lineales simultáneamente y admiten un tratamiento matricial. Para su resolución debe haber tantas ecuaciones como incógnitas y el determinante de la matriz ha de ser no nulo. Geométricamente corresponden a intersecciones de líneas en un único punto (Sistema lineal de dos ecuaciones con dos incógnitas), planos en una recta (dos ecuaciones lineales de tres incógnitas) o un único punto (tres ecuaciones lineales de tres incógnitas). Los casos en los que el determinante de la matriz es nulo no poseen solución.
Hay que puntualizar que a veces (particularmente en geometría), en un ejercicio, se pide resolver un sistema de ecuaciones que tiene menos ecuaciones que incógnitas, o cuyo determinante es nulo. En estos casos habrá incógnitas para los que no podamos encontrar ningún valor concreto (es decir, que no podremos decir "cuánto valen"). En estos casos, lo que hay que hacer es despejar esas incógnitas como si supiéramos sus valores, y considerarlas como parámetros. La solución es entonces no ya un punto, sino una recta, un plano, o en general una variedad lineal en el espacio afín asociado al espacio vectorial en el que trabajemos.
DETERMINAR LOS RESULTADOS DE UNA HOMOTECIA CUANDO LA RAZON ES IGUAL (febrero)

Una homotecia es una trasformación geométrica que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor. Es una amplificación. Su definición rigurosa es vectorial:
definición
Sea E un espacio vectorial sobre un cuerpo K. Sea Ω un elemento (visto como un punto) de E
La homotecia de centro Ω y de razón k, denotada hΩ, k envía un punto M del espacio vectorial sobre el punto M' tal que:
Homotecia, de centro el punto O y razón el número real k ≠ 0, es una transformación geométrica que hace corresponder a cada punto P otro punto P′ tal que (el vector es igual al resultado de multiplicar el vector por el número k). Si k es positivo, P′ está en la semirrecta de origen O que pasa por P.Veremos en lo siguiente las propiedades de la homotecia:
Propiedades
La homotecia es una trasformación lineal y por consiguiente conserva:
1.el alineamiento: las imágenes de puntos alineados son alineados: (A,B,C) y (A', B', C') en la figura
2.el centro de un segmento, y más generalmente el baricentro: la imagen del baricentro es el baricentro de las imágenes. En la figura, B es el centro de [A;C] y por lo tanto B' es el de [A';C']
3.el paralelismo: dos rectas paralelas tienen imágenes paralelas. En la figura (BE) // (CD) porque (BE) //(CD).
jueves, 20 de mayo de 2010
DETERMINAR EL TEOREMA DE TALES MEDIANTE CONSTRUCCIONES CON SEGMENTOS (enero)

Si varias rectas paralelas cortan a dos transversales, determinar en ellas segmentos correspondientes y proporcionales. Para poder resolver el teorema de tales es necesario repasar las propiedades de las proporciones. En toda proporcion la suma o diferencia de los antecedentes es a la suma o diferencia de los consecuentes, como cada antecedente a su consecuente.
En una proporcion el producto de los medios es igual al producto de los extremos, es decir, en una proporcion un medio es igual al producto de los extremos dividido entre otro.
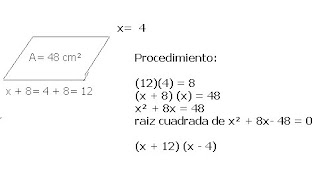
UTILIZAR ECUACIONES CUADRATICAS PARA MODELAR SITUACIONES Y RESOLVERLAS USANDO LA FORMULA GENERAL (enero)
Con el fin de mostrar el significado de las ecuaciones cuadráticas como modelo de situaciones y problemas, y su doble solución, se sugiere comenzar con problemas simples y aumentar poco a poco el nivel de complejidad. Por otra parte, se deberá observar que dependiendo del signo del discriminante (B2 – 4AC), una ecuación cuadrática puede tener dos soluciones reales, sólo una o ninguna solución real.
INTERPRETAR Y UTILIZA INDICES PARA EXPLICAR EL COMPORTAMIENTO DE DIVERSAS SITUACIONES. (diciembre)
EJEMPLO:
Entidad Federativa | 2002 | 2003 | 2004 |
PAIS | 7.4 | 7.4 | 7.4 |
hombres | 9.0 | 9.1 | 9.1 |
mujeres | 5.8 | 5.6 | 5.7 |
CAMPECHE | 8.5 | 9.2 | 9.75 |
hombres | 10.4 | 11.2 | 12.3 |
mujeres | 6.5 | 7.1 | 7.2 |
QUINTANA ROO | 6.9 | 6.7 | 6.3 |
hombres | 8.8 | 8.5 | 8.1 |
mujeres | 5.0 | 4.9 | 4.5 |
YUCATAN | 7.65 | 9.3 | 8.6 |
hombres | 9.6 | 11.5 | 10.6 |
mujeres | 5.7 | 7.0 | 6.6 |
____________________________________________
1.- ¿Como vario el indice de desercion en el 2004 respecto al 2002 en cada estado?
R: Pais es igual, Campeche 1.25, Quinana Roo bajo 0.6 y Yucatan subio 0.95.
2.- ¿Cual es el genero que presenta mayor desersion en cada estado el año 2004?
R: Hombres
3.- ¿Por que piensas que ocurre asi?
R: Porque varia mas
4.- ¿Que relacion hay entre los indices de cadaestado con el indice nacional?
R: De que en el nacional es igual y en los estados varian
5.- ¿Que sgerencias haria para disminuir los indices de desercion escolar?
R: Tratar de balancearlos
APLICACION DE SEMEJANZA DE TRIANGULOS (diciembre) :
1.- CALCULO DE ALTURAS A PARTIR DE LA SOMBRA.
La distancia del Sol a la Tierra es muy grande comparada con la tierra y con los objetos que hay sobre ella, de forma que podemos considerar que los rayos del Sol sobre objetos próximos son paralelos.(imagen 1)
Por ser los triángulos semejantes
(imagen 3)
Puedes variar la dirección de los rayos solares.
La semejanza de los triángulos ABC y A'B'C' permite calcular fácilmente a, (altura).
Ejercicio.
A una determinada hora de la tarde , para a' =0,50 m ; se tiene b'=0,38 m y b= 2,60 m. ¿Cuanto mide la distancia a= AB? Comprueba el resultado en la figura. para ajustar b' debes actuar en la dirección de los rayos solares.
2.- CALCULAR LA ALTURA SIN NECESIDAD DE SOMBRA.
Sitúa el objeto a' de forma que su extremo coincida con la semirrecta que parte de A (punto de observación).
En ese momento los triángulos son semejantes; por tanto (imagen 2)
¿Cuanto mide el árbol de la figura?
CRITERIOS DE SEMEJANZA DE TRIANGULOS(noviembre):
A. Criterio LLL. Dos triangulos son semejantes si msus tres lados son proporcionales.
B. Criterio LAL. Dos triangulos son semejantes si dos de sus lados son proporcionales y el angulo comprendido entre ellos es congruente.
C. Criterio ALA. Si dos ángulos y el lado entre ellos son respectivamente congruentes con los mismos de otro triángulo, entonces los triángulos son congruentes.
ejemplo de problemas de ecuaciones no lineales:
R: a 15x15=225-5=220
b) El cuadrado de un numero mas el mismo numero es igual a 306 ¿cuales ese numero?
R:17 x 17 = 289 + 17 = 306
c) El producto de dos numeros consecutivos es 552 ¿cuales son esos numeros?
R: 23 x 24 = 552
d) El volumen de un cubo es 100cm3 ¿cual es la medida de su arista?
R: 4.64158883433= 100
e) El cuadrado de un numero es igual al triple del mismo, de que numero se trata:
R: x²= 3x 32=(3)(3)=9
f) El cubo de un numero es igual a 343 cual es ese numero:
R: x3= 343 73=343
g) El cuadrado de un numero menos el doble del mismo numero es igual a 24 cual es ese numero:
R: x²- 2x=24 6x6-12=24
h) El cuadrado de un numero es igual a la tercera parte del mismo mas 8, cual es ese numero:
R: x²= x/3 + 8 3x3= 9/3=3
i) La mitad de un numero mas el cubo de dicho numero es igual a 9, cual es ese numero:
R: x/2 + x3 =9 X=2
ECUACIONES NO LINEALES(noviembre):
sistema
La resolución de estos sistemas se suele hacer por el método de sustitución, para ello seguiremos los siguientes pasos:
1º Se despeja una incógnita en una de las ecuaciones, preferentemente en la de primer grado.
y = 7 − x
2º Se sustituye el valor de la incógnita despejada en la otra ecuación.
x2 + (7 − x)2 = 25
3º Se resuelve la ecuación resultante.
x2 + 49 − 14x + x2 = 25
2x2 − 14x + 24 = 0
x2 − 7x + 12 = 0
solución
4º Cada uno de los valores obtenidos se sustituye en la otra ecuación, se obtienen así los valores correspondientes de la otra incógnita.
x = 3 y = 7 − 3 y = 4
x = 4 y = 7 − 4 y = 3
RAZON DE CAMBIO(octubre):
con respecto a otra variable, para una función y = f (x) , se podría obtener la
derivada o razón de cambio de las variables " x " y " y " con respecto al tiempo
" t ", es decir: "
dt
dy " y "
dt
dx ". Lo cual nos va a permitir resolver problemas de
aplicación.
EJEMPLO:
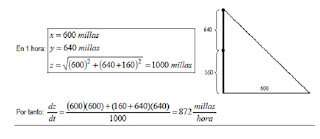
Un aeroplano que vuela hacia el norte a 640 millas/h pasa sobre cierta ciudad al medio
día (12h00). Un segundo aeroplano que va hacia el este a 600 millas/h, esta
directamente encima de la misma ciudad 15 min. mas tarde. Si los aeroplano están
volando a la misma altitud, que tan rápido se están separando a la 1:15 p.m.(13h15).
SOLUCIÓN:
domingo, 16 de mayo de 2010
ANGULO INSCRITO Y CENTRAL:(octubre)

El angulo central es aquel que esta formado por dos radios y cuyo vertice es el centro de la circunferencia.
El angulo inscrito es el angulo que esta formado por dos cuerdas y cuyo vertice es cualquier punto de la circunferencia.
Las caracteristicas de estos angulos es que el angulo central mide el doble que el angulo inscrito.
ELEMENTOS DE UNA CIRCUNFERENCIA:(septiembre)
b)Cuerda: es el segmento de recta que une a dos puntos de la circunferencia.
c)Diametro: es la cuerda mayor dentro de la circunferencia, pasa por el centro de la misma y su medida siempre es el doble del radio.
d)Arco: es una porcion de la circunferencia.
e)Secante: es una linea que atravieza la circunferencia y la corta en dos puntos.
f)Tangente: es una linea recta exterior a la circunferencia que la toca solo en un punto.
sábado, 15 de mayo de 2010
FACTORIZAR EXPRESIONES ALGEBRAICAS:(septiembre)
1.- Se multiplica el trinomio por el coeficiente de la x²:
6(6x²)-6(7x)-6(3)
36x² -6(7x) -18 -> (6x-9)(6x+2)
* se efectua las multiplicaciones del 1er y 3er termino y el segundo termino se deja expresado en factores.
2.- Factorizar la expresion resultante de la (x).
36x² = (6x)(6x)
(-9)(+2) = -18
(-9+2) = -7
3.- Se divide los dos factores entre el coeficiente por el cual multiplicamos:
(6x-9)(6x+2)
_____________
6
4.- Se descompone en factores el coeficiente:
(6x-9)(6x+2)
____________
(3)(2)
5.- Se toma el factor correspondiente para efectuar divisiones exactas:
(6x-9) (6x+2)
_______ ________
3 2
RESULTADO = (2x-3)(3x+1)